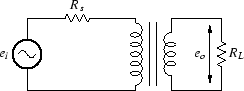 |
前節で作成したSPICEによるトランスのモデルを使用して, 利得・位相・インピーダンスの周波数特性を解析します.
まず,信号源抵抗 Rs をさまざまに変化させたときの, トランスの周波数特性を調べます. 回路は,図5.15のようになります. Rs = 1.25 kΩ は,三極管を使用した場合, Rs = 2.5 kΩ は,カタログ等に記載されている周波数特性, Rs = 10 kΩ は,多極管を使用した場合に相当します.
利得の周波数特性を図5.16に, 位相の周波数特性を図5.17に示します. 使用したSPICEのソースプログラムは,以下のとおりです.
1 OPT frequency response
2 .INCLUDE OPT2k5.inc
3
4 VI 1 0 DC 0 AC 1V
5
6 RS1 1 11 1.25k
7 XOPT1 11 0 12 0 OPT2k5
8 RL1 12 0 8
9
10 RS2 1 21 2.5k
11 XOPT2 21 0 22 0 OPT2k5
12 RL2 22 0 8
13
14 RS3 1 31 10k
15 XOPT3 31 0 32 0 OPT2k5
16 RL3 32 0 8
17
18 RS4 1 41 1k
19 XOPT4 41 0 42 0 OPT2k5
20
21 RS5 1 51 1k
22 XOPT5 51 0 0 0 OPT2k5
23
24 .control
25 set width=160
26 ac dec 50 1 1Meg
27 *plot db(v(12)) db(v(22)) db(v(32))
28 *plot ph(v(12)) ph(v(22)) ph(v(32))
29 *plot db(v(21)/v(21,1)*2.5e3) db(v(41)/v(41,1)*1e3) db(v(51)/v(51,1)*1e3)
30 *print v(12) v(22) v(32)
31 *print v(21)/v(21,1)*2.5e3 v(41)/v(41,1)*1e3 v(51)/v(51,1)*1e3
32 .endc
33 .END
図5.16では,1kHz における eo を 0dB としてグラフを描いています. 信号源抵抗が低いと,低域が伸び,高域が下がります. 信号源抵抗が高いと,低域が下がり,高域にピークが生じます. ピークを超えると,レスポンスは急激に下がります.
低域の等価回路より,
| eo | = | ei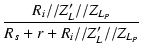 |
|
| = | 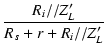 . . 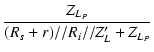 |
||
| = | 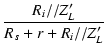 . . 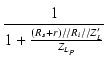 |
||
| = | 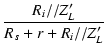 . . 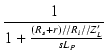 |
(5.55) |
| Tl | = | 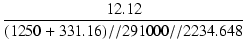 = 0.01313 [s] = 0.01313 [s] |
|
| fl | = | 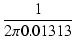 = 12.12 [Hz] = 12.12 [Hz] |
| Tl | = | 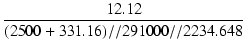 = 0.009746 [s] = 0.009746 [s] |
|
| fl | = | 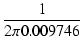 = 16.33 [Hz] = 16.33 [Hz] |
| Tl | = | 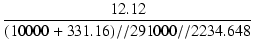 = 0.006638 [s] = 0.006638 [s] |
|
| fl | = | 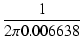 = 23.97 [Hz] = 23.97 [Hz] |
負荷抵抗 RL を公称値(8 Ω),開放,短絡としたときの, 1次インピーダンスの周波数特性を図5.18に示します. 図5.11の実測結果がよく再現されていることがわかります.
利得の周波数特性を図5.19に, 位相の周波数特性を図5.20に示します.
Rs = 2.5 kΩ は,三極管を使用した場合, Rs = 5 kΩ は,カタログ等に記載されている周波数特性, Rs = 50 kΩ は,多極管を使用した場合に相当します.
F-2021の場合,出力管の内部抵抗が変化しても,高域にピークが生じません. カタログに,「どのような出力管とも組み合わせることができます」, と書いてあるのは,信じてよいようです.
使用したSPICEのソースプログラムは,以下のとおりです.
1 OPT frequency response
2 .INCLUDE F2021.inc
3
4 VI 1 0 DC 0 AC 1V
5
6 RS1 1 11 2.5k
7 XOPT1 11 10 10 0 12 0 F2021
8 RL1 12 0 8
9
10 RS2 1 21 5k
11 XOPT2 21 20 20 0 22 0 F2021
12 RL2 22 0 8
13
14 RS3 1 31 40k
15 XOPT3 31 30 30 0 32 0 F2021
16 RL3 32 0 8
17
18 RS4 1 41 1k
19 XOPT4 41 0 43 0 42 0 F2021
20
21 RS5 1 51 1k
22 XOPT5 51 0 53 0 0 0 F2021
23
24 RS6 1 61 1k
25 XOPT6 61 0 0 0 62 0 F2021
26
27 .control
28 set width=180
29 ac dec 50 1 1Meg
30 *plot db(v(12)) db(v(22)) db(v(32))
31 *plot ph(v(12)) ph(v(22)) ph(v(32))
32 *plot db(v(21)/v(21,1)*5e3) db(v(41)/v(41,1)*1e3) db(v(51)/v(51,1)*1e3) db(v(61)/v(61,1)*1e3)
33 *print v(12) v(22) v(32)
34 *print v(21)/v(21,1)*5e3 v(41)/v(41,1)*1e3 v(51)/v(51,1)*1e3 v(61)/v(61,1)*1e3
35 .endc
36 .END
1次インピーダンスの周波数特性を図5.21に示します.