Next: 5.4 SEPPの打ち消し回路 Up: 5. 並列合成プッシュプル Previous: 5.2 並列合成プッシュプル出力段の設計
マッキントッシュに代表されるCSPP回路では, 原理的には真空管のグリッド-カソード間に入力を加えますが, 実際の回路でそれを実現するのは,段間トランスを使う場合を除いては困難であり, 一般に対グラウンドでグリッドに信号を与えます. そのようにすると,各真空管には出力の50%の帰還がカソードにかかり, 半カソードフォロアとして働きます. それに伴い,大きな励振電圧が必要になり, 高いドライブ電圧を得るために ドライブ段にブートストラップが用いられることが多くなります. CSPP出力段とドライブ段を同時に解析することにより, 回路設計の指針を得ることが本節の目的です.
等価回路より,
| eg1 | = | e2 + e3 | (5.1) |
| eo | = | - gm1eg1(rp1//RL1) | (5.2) |
| e3 | = | (5.3) |
| eg1 | = | e2 + |
|
| eo | = | - gm1(rp1//RL1) |
|
| = | - gm1(rp1//RL1)e2 | ||
| eo | = | - 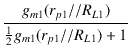 e2 e2 |
|
A1 |
(5.5) |
A1 = - 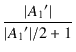
|
(5.6) |
|
F = |
(5.7) |
| eg1 | = | (5.8) | |
| i1 | = | gm1eg1 = |
(5.9) |
| i2 | = | (5.10) | |
| i | = | i1 + i2 = |
(5.11) |
|
Zo = rp1// |
(5.14) |
|
Zo |
(5.15) |
プレート特性図とロードラインは,図5.21のようになります.
出力段のゲインは,式(5.4)より,
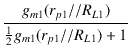 = -
= - 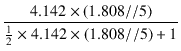 = - 1.467
= - 1.467
負帰還量は,
となります.
出力インピーダンスは,
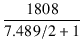 = 381.1
= 381.1 となります.
尖頭値が87.414Vの入力を加えた時, カソードの電圧は67.414Vとなりますので, グリッド電圧は -20 + 87.414 - 67.414 = 0 V となり, フルスイング状態になります. このときのプレート電圧は115.2V,プレート電流は66.45mAとなります. -87.414 Vの入力を加えた時, カソードの電圧は-60.710 Vとなりますので, グリッド電圧は -20 - 87.414 + 60.71 = - 46.704 V となります. グリッドバイアス-20 Vの2倍とはならないことに注意してください. 入力の負側では出力波形が潰れるので,カソードに生じる負の電圧が小さくなり, 入力の打ち消しが少なくなるためです. このときのプレート電圧は371.4V,プレート電流は15.20mAとなります. 出力電圧(プレート電圧)の実効値は90.65V, 出力電力は 90.652/5000 = 1.643 W , 歪率は2.62%でした.
プレート特性図とロードラインは,図5.22のようになります.
出力段のゲインは,
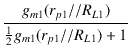 = -
= - 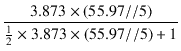 = - 1.798
= - 1.798
負帰還量は,
となります.
出力インピーダンスは,
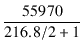 = 511.7
= 511.7 となります.
尖頭値が110.08Vの入力を加えた時, カソードの電圧は100.0Vとなりますので, グリッド電圧は -20 + 110.08 - 100.0 = - 9.92 V となります. このときのプレート電圧は50.00V,プレート電流は76.92mAとなります. -110.08 Vの入力を加えた時, カソードの電圧は-89.47 Vとなりますので, グリッド電圧は -20 - 110.08 + 89.47 = - 40.61 V となります. 三極管接続の場合と同じように,入力のマイナス側で グリッド電圧の波形が伸びるようになります. このときのプレート電圧は428.9V,プレート電流は1.13mAとなります. 出力電圧(プレート電圧)の実効値は136.2V, 出力電力は 136.22/5000 = 3.712 W , 歪率は2.97%でした.
尖頭値が87.24Vの入力を加えた時の各部の波形を, 図5.26に示します.
図より,出力電圧の実効値が90.72Vなので, 出力は Po = Vo2/RL = 90.722/5000 = 1.646 W となりました.出力インピーダンスを求めるシミュレーション回路を, 図5.27に示します.
AC解析の結果を, 図5.28に示します. 図より,出力インピーダンスは 381.1Ω となりました.
尖頭値が110.08Vの入力を加えた時の各部の波形を, 図5.31に示します. この入力電圧は,プレート-カソード間の最小電圧が50Vとなる電圧です.
図より,出力電圧の実効値が136.4Vなので, 出力は Po = Vo2/RL = 136.42/5000 = 3.721 W となりました. ビーム管接続のネイティブ動作の場合,出力は2.9W程度でしたが, それよりはるかに大きな出力が得られています. カソード帰還により,出力波形に含まれる2次歪が減っており, プレート-カソード間の電圧が高くなる場合に潰れていた波形が伸びたため, 出力が大きくなったものです.出力インピーダンスを求めるシミュレーション回路を, 図5.32に示します.
AC解析の結果を, 図5.33に示します. 図より,出力インピーダンスは 511.7Ω となりました.
等価回路より,
この式をさらに変形していくと,
| A2 | = | - gm2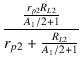 = - gm2 = - gm2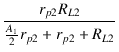 = - gm2 = - gm2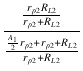 |
|
| = | - gm2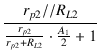 |
等価回路より,
| eg1 | = | e2 + e3 | (5.22) |
| eo | = | - |
(5.23) |
| e3 | = | (5.24) |
等価回路より,
| eg1 | = | e2 + |
(5.26) |
| i1 | = | gm1eg1 | (5.27) |
| i2 | = | (5.28) | |
| e2 | = | - |
(5.29) |
|
Zo = rp1// |
(5.32) |
|
Zo |
(5.33) |
入力に,87.8007Vを加えた時, プレート電圧は114.3986Vとなり, 250 - 114.3986 = 135.6014 V 下降します. この半分がカソード電圧の上昇となり,カソードの電圧は67.8007Vとなります. グリッド電圧は 87.8007 - 67.8007 - 20 = 0 V となって, フルスイングの状態です. このとき,プレート電流は65.8354mAで, 65.8354 - 39.4842 = 26.3512 mA 増えています. 5 kΩ のロードラインによる電流の増加は, 135.6014/5 = 27.1203 mA となるはずですから, したがって,ドライブ段のプレート電流の変化(減少)は 0.7691 x 2 = 1.5382 mA です.
同様に,入力に -87.8007 V を加えた時, プレート電圧は372.6701Vとなり, 372.6701 - 250 = 122.6701 V 上昇します. この半分がカソード電圧の下降となり,カソードの電圧は -61.3350 V となります. グリッド電圧は -87.8007 + 61.3350 - 20 = - 46.4657 V となります. このとき,プレート電流は15.9681mAで, 39.4842 - 15.9681 = 23.5161 mA 減っています. 5 kΩ のロードラインによる電流の減少は, 122.6701/5 = 24.5340 mA となるはずですから, 差の 24.5340 - 23.5161 = 1.0179 mA がドライブ段のプレート電流の変化の半分ということになります. したがって,ドライブ段のプレート電流の変化(増加)は 1.0179 x 2 = 2.0358 mA です.
このように,出力段に対称な波形を加えた時であっても, 出力の波形は対称にならず,それがカソードに帰還されるため, グリッド電圧の波形も対称にならず,ロードライン(水色)はわずかに湾曲します. この場合の例では,プラスの入力の時にグリッド電圧は20V上昇し, マイナスの入力の時に26.4657V下降していることになります.
実際には,ドライブ段に対称な波形を加えても, ドライブ段の出力には歪んだ波形が生じるので, 状況はさらに複雑になります.
出力段のゲインは,式(5.25)より,
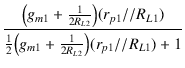 = -
= - 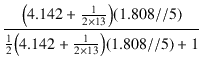 = - 1.470
= - 1.470
となります.
このとき,ドライブ段の負荷抵抗は,ブートストラップにより,
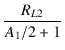 =
= 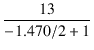 = 49.06 [kΩ]
= 49.06 [kΩ]
となるため,交流負荷は 49.06//100 = 32.92 kΩ となります.
ドライブ段のプレート特性図とロードラインは, 図5.39のようになります.
緑色の線は 13 kΩ の直流ロードライン, 青色の線は交流ロードラインです. ブートストラップがないときの交流ロードラインは破線で示してあります.出力段のグリッド抵抗は,ブートストラップされていないので,ドライブ段の内部抵抗と並列に接続されるとして計算します. したがって,ここでは rp2 = 13.44//100 = 11.84 kΩ として計算します.
ドライブ段のゲインは,式(5.20)より,
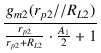 = -
= - 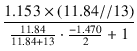 = - 11.00
= - 11.00
PFB量は,式(5.21)より,
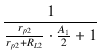 =
= 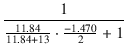 = 1.540 = 3.75 dB
= 1.540 = 3.75 dB
となります.
出力インピーダンスは,式(5.34)より,
| Zo | = | rp1//4(rp2 + RL2)// |
|
| = | 1808//4 x (11, 840 + 13, 000)//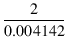 |
水色の線は,尖頭値が9.3189Vの入力を加えた時の, 出力段の非線形性を考慮に入れたドライブ段のロードラインです. これは,ドライブ段のプラス側の出力が87.8Vとなる入力電圧です. これにより,出力段のグリッド電圧が0Vとなります. 一方で,マイナス側の振幅は120.7Vとなりますが, カットオフには至らないようです.
動作点付近では,青色の線と水色の線が接していますが, 水色の線はやや弓なりに反っています. このときのドライブ段の歪率は7.92%, 出力の歪率は4.71%ですので, ドライブ段と出力段で歪の打ち消しが起こっていますが, ドライブ段の歪率が優勢となっています. 出力段の出力電圧は106.2V, 出力は2.257Wとなりました.
出力段のゲインは,式(5.25)より,
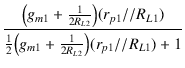 = -
= - 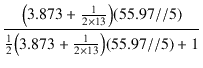 = - 1.800
= - 1.800
となります.
このとき,ドライブ段の負荷抵抗は,ブートストラップにより,
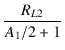 =
= 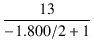 = 129.7 [kΩ]
= 129.7 [kΩ]
となるため,交流負荷は 129.7//100 = 56.47 kΩ となります.
ドライブ段のプレート特性図とロードラインは, 図5.41のようになります.
緑色の線は 13 kΩ の直流ロードライン, 青色の線は交流ロードラインです. ブートストラップがないときの交流ロードラインは破線で示してあります.ドライブ段のゲインは,
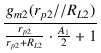 = -
= - 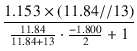 = - 12.51
= - 12.51
PFB量は,
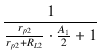 =
= 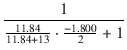 = 1.750 = 4.86 dB
= 1.750 = 4.86 dB
となります.
出力インピーダンスは,
| Zo | = | rp1//4(rp2 + RL2)// |
|
| = | 55, 970//4 x (11, 840 + 13, 000)//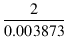 |
水色の線は,尖頭値が8.16Vの入力を加えた時の, 出力段の非線形性を考慮に入れたドライブ段のロードラインです. ドライブ段の2次歪により,出力段には負側が伸びた波形が加えられるため, プレート電圧の最低値が50Vに達する前にカットオフしてしまいます. 動作点付近では,青色の線と水色の線が接していますが, 水色の線はやや弓なりに反っています. このときのドライブ段の歪率は3.86%, 出力の歪率は1.86%ですので, ドライブ段と出力段で歪の打ち消しが起こっていますが, ドライブ段の歪率が優勢となっています. 出力段の出力電圧は126.8V, 出力は3.215Wとなりました.
プレート損失には余裕があるため, バイアスを浅くすれば,より大きな出力を得られます.
出力段のゲインは,式(5.25)より,
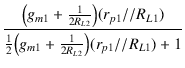 = -
= - 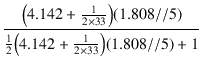 = - 1.468
= - 1.468
となります.
このとき,ドライブ段の負荷抵抗は,ブートストラップにより,
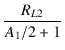 =
= 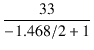 = 123.7 [kΩ]
= 123.7 [kΩ]
となるため,交流負荷は 123.7//100 = 55.31 kΩ となります.
ドライブ段のプレート特性図とロードラインは, 図5.43のようになります.
緑色の線は 33 kΩ の直流ロードライン, 青色の線は交流ロードラインです. ブートストラップがないときの交流ロードラインは破線で示してあります.計算上の内部抵抗は rp2 = 2378//100 = 95.96 kΩ として計算します.
ドライブ段のゲインは,
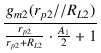 = -
= - 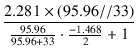 = - 123.3
= - 123.3
PFB量は,
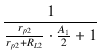 =
= 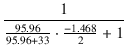 = 2.201 = 6.85 dB
= 2.201 = 6.85 dB
となります.
出力インピーダンスは,
| Zo | = | rp1//4(rp2 + RL2)// |
|
| = | 1808//4 x (95, 960 + 33, 000)//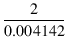 |
水色の線は,尖頭値が0.8736Vの入力を加えた時の, 出力段の非線形性を考慮に入れたドライブ段のロードラインです. 動作点付近では,青色の線と水色の線が接していますが, 水色の線はやや弓なりに反っています. このときのドライブ段の歪率は7.15%, 出力の歪率は4.39%ですので, ドライブ段と出力段で歪の打ち消しが起こっていますが, ドライブ段の歪率が優勢となっています. 出力段の出力電圧は106.1V, 出力は2.250Wとなりました.
出力段のゲインは,式(5.25)より,
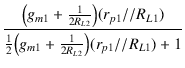 = -
= - 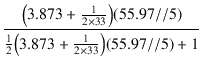 = - 1.798
= - 1.798
となります.
このとき,ドライブ段の負荷抵抗は,ブートストラップにより,
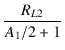 =
= 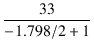 = 326.3 [kΩ]
= 326.3 [kΩ]
となるため,交流負荷は 326.3//100 = 76.54 kΩ となります.
ドライブ段のプレート特性図とロードラインは, 図5.45のようになります.
緑色の線は 33 kΩ の直流ロードライン, 青色の線は交流ロードラインです. ブートストラップがないときの交流ロードラインは破線で示してあります.計算上の内部抵抗は rp2 = 2378//100 = 95.96 kΩ として計算します.
ドライブ段のゲインは,
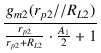 = -
= - 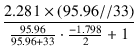 = - 169.1
= - 169.1
PFB量は,
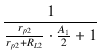 =
= 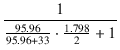 = 3.020 = 9.60 dB
= 3.020 = 9.60 dB
となります.
出力インピーダンスは,
| Zo | = | rp1//4(rp2 + RL2)// |
|
| = | 55, 970//4 x (95, 960 + 33, 000)//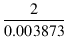 |
水色の線は,尖頭値が0.6851Vの入力を加えた時の, 出力段の非線形性を考慮に入れたドライブ段のロードラインです. 動作点付近では,青色の線と水色の線が接していますが, 水色の線はやや弓なりに反っています. このときのドライブ段の歪率は4.31%, 出力の歪率は4.42%でした. 出力段の出力電圧は132.5V, 出力は3.512Wとなりました.
出力インピーダンスを求めるシミュレーション回路を, 図5.48に示します.
以下,出力インピーダンスを求めるシミュレーション回路は, ゲインを求める回路から負荷抵抗RL1を取り除き,そこに1Aの電流源を入れ, 入力の電圧源を除去して短絡したものですので,省略します. AC解析の結果を, 図5.49に示します. 図より,出力インピーダンスは607.2Ω となりました.
出力インピーダンスのAC解析の結果を, 図5.52に示します.
図より,出力インピーダンスは960.6Ω となりました.
出力インピーダンスのAC解析の結果を, 図5.55に示します.
図より,出力インピーダンスは921.9Ω となりました.
出力インピーダンスのAC解析の結果を, 図5.58に示します.
図より,出力インピーダンスは1.940kΩ となりました.
そこで,一般的な場合にPFBや出力インピーダンスがどのように変化するかをつかむため, RL2 を rp2 の何倍にするかを横軸に, PFBや出力インピーダンスを縦軸にとって,グラフにしてみました(図5.59).
赤い線がPFBで,PFBは出力段のゲインによって変わるので, | A1| が1.4, 1.6, 1.8, 2.0の場合について描いてあります. 出力段が三極管の場合は1.4から1.6, 多極管の場合は1.6から1.8程度が参考になるでしょう.
青い線が出力インピーダンスの様子を表しており,
縦軸の目盛りは,1/gm1
(カソードフォロワとしたときの出力インピーダンス)を1としています.
または,縦軸の値を gm1
で割れば,出力インピーダンスが求められます.
出力インピーダンスは出力段の増幅率によって変わるので,
![]() が5, 10, 100,
が5, 10, 100, ![]() の場合について描いてあります.
出力段が三極管の場合は5から10,
多極管の場合は100程度が参考になるでしょう.
の場合について描いてあります.
出力段が三極管の場合は5から10,
多極管の場合は100程度が参考になるでしょう.
なお,rp2 にはドライブ段の真空管の内部抵抗と, 出力段のグリッド抵抗の並列合成値を使ってください.
先ほどの12AU7の例では, rp2 = 13.44//100 = 11.84 kΩ , RL2 = 13 kΩ ですから, 横軸は1.1程度になります.
6AU6の例では, rp2 = 2378//100 = 96 kΩ , RL2 = 33 kΩ ですから, 横軸は0.34程度になります.
ayumi