Next: 3.3 カソード結合型(ミュラード型) Up: 3. 位相反転回路 Previous: 3.1 P-K分割

3.2 差動増幅回路

位相反転回路としては，差動増幅回路よりは，次節のミュラード型のほうがよく使われますが，差動増幅回路のほうが解析が簡単なので，こちらから先に説明します．

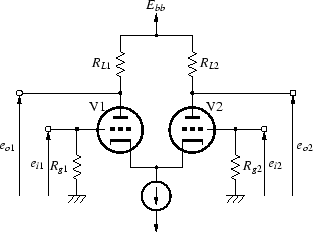
差動増幅回路は，2本の真空管のカソードを結び，そこに定電流源を接続して， 2本の真空管のプレート電流の和を常に一定に保つようにした回路です(図3.10)．

**図 3.10:** 差動増幅回路
$\begin{figure}\input{figs/diff} \end{figure}$

プレート電流の和が一定ですから，片方の真空管のプレート電流が増えると，その分だけもう一方の真空管のプレート電流が減ります．負荷抵抗が等しければ，正確に位相が反転した電圧がプレートに現われます．差動増幅回路には，2つの入力があります．出力には，2つの入力の差のみが現われます．位相反転回路として使用する場合は，一方の入力のみを使い，他方はアースするか，負帰還の入力として使用します．

3.2.1 ゲイン

差動増幅回路の等価回路は図3.11のようになります．定電流源は交流的には開放となります．等価回路より，次の関係が成り立ちます．

**図 3.11:** 差動増幅回路の等価回路
$\begin{figure}\input{figs/diff_equiv} \end{figure}$

e_o1	=	iR_L	(3.17)
e_o2	=	- iR_L	(3.18)
- μ(e_g1 - e_g2)	=	2i(r_p + R_L)	(3.19)
e_k	=	μe_g1 + i(r_p + R_L) = μe_g2 - i(r_p + R_L)	(3.20)
e_i1	=	e_g1 + e_k	(3.21)
e_i2	=	e_g2 + e_k	(3.22)

これより，

e_g1	=	e_i1 - e_k = e_i1 - i(r_p + R_L) - μe_g1
(1 + μ)e_g1	=	e_i1 - (r_p + R_L)i
e_g1	=	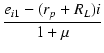$\displaystyle {\frac{{e_{i1}-(r_p+R_L)i}}{{1+\micro}}}$
e_g2	=	e_i2 - e_k = e_i2 + i(r_p + R_L) - μe_g2
(1 + μ)e_g2	=	e_i2 + (r_p + R_L)i
e_g2	=	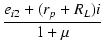$\displaystyle {\frac{{e_{i2}+(r_p+R_L)i}}{{1+\micro}}}$
2i(r_p + R_L)	=	- μ(e_g1 - e_g2)
	=	- $\displaystyle {\frac{{\micro}}{{1+\micro}}}$ {e_i1 - e_i2 -2(r_p + R_L)i}
2(r_p + R_L)i	=	- μ(e_i1 - e_i2)
i	=	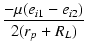$\displaystyle {\frac{{-\micro(e_{i1}-e_{i2})}}{{2(r_p+R_L)}}}$
e_o1	=	iR_L = - μ(e_i1 - e_i2)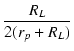 $\displaystyle {\frac{{R_L}}{{2(r_p+R_L)}}}$	(3.23)
e_k	=	i(r_p + R_L) + μe_g1 = (r_p + R_L)i + μ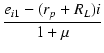 $\displaystyle {\frac{{e_{i1}-(r_p+R_L)i}}{{1+\micro}}}$
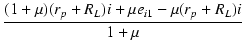	=	$\displaystyle {\frac{{(1+\micro)(r_p+R_L)i+\micro e_{i1}-\micro(r_p+R_L)i}}{{1+\micro}}}$
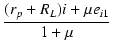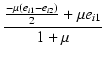	=	$\displaystyle {\frac{{(r_p+R_L)i+\micro e_{i1}}}{{1+\micro}}}$ = $\displaystyle {\frac{{\frac{-\micro(e_{i1}-e_{i2})}{2}+\micro e_{i1}}}{{1+\micro}}}$
	=	$\displaystyle {\frac{{\micro}}{{1+\micro}}}$ ^. $\displaystyle {\frac{{e_{i1}+e_{i2}}}{{2}}}$	(3.24)

したがって，差動増幅回路の片側の出力のゲインは，通常のカソード接地回路のゲインの1/2になります．出力を両プレート間から取り出せば，カソード接地回路と同じ増幅度が得られます．また，カソードには， ( μ $\gg$ 1 のとき)入力電圧の平均値とほぼ等しい電圧が現われています．

3.2.2 出力インピーダンス

差動増幅回路の出力インピーダンスを求めるための等価回路は図3.12のようになります．等価回路より，次の関係が成り立ちます．

**図 3.12:** 差動増幅回路の出力インピーダンスを求めるための等価回路
$\begin{figure}\input{figs/diff_zo} \end{figure}$

i₁	=	$\displaystyle {\frac{{e_o}}{{R_L}}}$	(3.25)
e_o + μ(e_g1 - e_g2)	=	i₂(2r_p + R_L)	(3.26)
e_g1	=	e_g2 = - e_k	(3.27)

これより，

i₂	=	$\displaystyle {\frac{{e_o}}{{2r_p+R_L}}}$
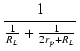Z_o	=	$\displaystyle {\frac{{e_o}}{{i_1+i_2}}}$ = $\displaystyle {\frac{{1}}{{\frac{1}{R_L}+\frac{1}{2r_p+R_L}}}}$
	=	R_L//(2r_p + R_L)

となります．

また，両方の出力の条件が等しい場合の出力インピーダンスを求めるための等価回路は図3.13のようになります．等価回路より，

**図 3.13:** 差動増幅回路の出力インピーダンスを求めるための等価回路(負荷の条件が等しい場合)
$\begin{figure}\input{figs/diff_zo_bal} \end{figure}$

i₁	=	$\displaystyle {\frac{{e_o}}{{R_L}}}$	(3.28)
2e_o + μ(e_g1 - e_g2)	=	2i₂r_p	(3.29)
e_g1	=	e_g2	(3.30)

これより，

i₂	=	$\displaystyle {\frac{{e_o}}{{r_p}}}$
Z'_o	=	$\displaystyle {\frac{{e_o}}{{i_1+i_2}}}$ = r_p//R_L

となり，カソード接地と同じです．高域特性を調べる場合には，この Z'_o を使います．

ここでは，12AU7を使った差動増幅回路を解析します．対グリッド電源電圧 E_bb = 256 V, 負荷抵抗 R_k = R_p = 33 kΩ, 共通カソード電流 I_k = 6.53632 mA とします．動作点は， E_p = 142.1451 V, E_g = - 6.00566 V で，この動作点における三定数は， g_m = 1388.774 μS, r_p = 11.75587 kΩ, μ = 16.32624 です．

\| A\|	=	16.32624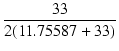 $\displaystyle {\frac{{33}}{{2(11.75587+33)}}}$ = 6.018942
Z_o	=	33//(2 `x` 11.75587 + 33) = 20.834 [kΩ]
Z'_o	=	33//11.75587 = 8.667995 [kΩ]

図3.14に， V1およびV2のプレートとアース間に 100 pF または 0.01 μF を付加した場合の周波数特性を示します．赤い線がV1側のゲイン，青い線がV2側のゲインを表わしています．実線は，V1，V2とも 100 pF を付加した場合，破線は，V1に 0.01 μF, V2に 100 pF を付加した場合，点線は，V1，V2とも 0.01 μF を付加した場合です． 0.01 μF を付加した場合のカットオフ周波数は，

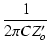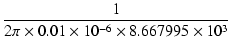f_c = $\displaystyle {\frac{{1}}{{2 \pi C Z'_o}}}$ = $\displaystyle {\frac{{1}}{{2 \pi \times 0.01 \times 10^{-6} \times 8.667995 \times 10^3}}}$ = 1836.122 [Hz]

となり，グラフと一致しています．

**図 3.14:** 差動増幅回路の周波数特性(1)
$\includegraphics{figs/diff1.ps}$

V1側に 220 pF, V2側に 200 pF を付加した場合の周波数特性は図3.7のようになります． V1とV2で多少形が異なりますが， P-K分割回路と比べると素直な落ち方になっています．

**図 3.15:** 差動増幅回路の周波数特性(2)
$\includegraphics{figs/diff2.ps}$

3.2.4 シミュレーション例

さきほどの数値例の定数を使い，SPICEでシミュレートします．回路は，図3.16のとおりです．

**図 3.16:** 差動増幅回路(シミュレーション用)
$\begin{figure}\input{figs/diff_spice} \end{figure}$

3.2.4.1 `diff.cir`

    1 Differential amplifier with 12AU7
    2 .INCLUDE 12AU7.lib
    3 X1 1 2 3 12AU7
    4 X2 4 5 3 12AU7
    5 IK 3 0 6.53632mA
    6 RL1 6 1 33k
    7 RL2 6 4 33k
    8 RG1 2 0 470k
    9 RG2 5 0 470k
   10 VI 2 0 DC 0V AC 1V
   11 VBB 6 0 256V
   12 .control
   13 op
   14 print v(1) v(3) v(1,3) v(2,3) v(4,3) v(5,3) i(vbb)
   15 tf v(1) vi
   16 print all
   17 tf v(4) vi
   18 print all
   19 ac dec 1 1k 1k
   20 print v(2) v(3)
   21 .endc
   22 .END

3.2.4.2 結果

    1 
    2 Circuit: Differential amplifier with 12AU7
    3 
    4 v(1) = 1.481507e+02
    5 v(3) = 6.005662e+00
    6 v(1,3) = 1.421451e+02
    7 v(2,3) = -6.00566e+00
    8 v(4,3) = 1.421451e+02
    9 v(5,3) = -6.00566e+00
   10 i(vbb) = -6.53632e-03
   11 transfer_function = -6.01894e+00
   12 output_impedance_at_v(1) = 2.083400e+04
   13 vi#input_impedance = 4.700000e+05
   14 transfer_function = 6.018939e+00
   15 output_impedance_at_v(4) = 2.083400e+04
   16 vi#input_impedance = 4.700000e+05
   17 v(2) = 1.000000e+00,0.000000e+00
   18 v(3) = 4.716081e-01,1.373463e-02

3.2.5 設計

カソードには，入力の約1/2の電圧が生じるので，それだけカソード電圧が変動しても定電流回路が正しく動作することを保証する必要があります．カソード電圧が決まれば， E_bb - E_k を電源電圧とするカソード接地回路と同様に設計を進めます．所要入力電圧は，カソード接地回路の2倍となります．

差動増幅回路は，動特性曲線の非直線性を打ち消すようにカソード電圧が変化するので，プレート電流が変化する範囲はカソード接地回路よりも狭くなります．

差動増幅回路による位相反転のロードラインは，図3.17のようになります．青い線が負荷抵抗 33 kΩ によるロードラインで， x 軸との交点は E_bb = 256 V にとってあるので，各球の対アースプレート電圧を表わします． V1のロードラインは緑色の線(丸印がついている曲線)で， V2のロードラインは茶色の線です． V1のプレート電流とカソード電圧の関係は，オレンジ色の線で表わされています．

**図 3.17:** 差動増幅回路のロードライン
$\includegraphics{figs/diff3.ps}$

例えば e_i = 10 V の入力があった場合，カソード電圧は E_k = 11.3 V となり， V1のグリッド電圧は E_g1 = 10 - 11.3 = - 1.3 V となって，プレート電流が I_p1 = 5.09 mA 流れます．このときのプレート電圧は E_p1 = 76.8 V で，対アースプレート電圧は E_o1 = 88.0 V になります． V2のグリッド電圧は E_g2 = 0 - 11.3 = - 11.3 V となって，プレート電流が I_p2 = 1.45 mA 流れます．このときのプレート電圧は E_p2 = 197.0 V で，対アースプレート電圧は E_o2 = 208.3 V になります．プレート電流の合計は 5.09 + 1.45 = 6.54 mA となって，設定したカソード電流と確かに一致しています．

また，V1のロードラインと E_g = 0 の交点は，約 13.35 V なので，尖頭値で 13.35 V までの入力を加えることができます．

伝達特性のグラフは，以下に示すRの関数 trans.diff を使用して作成できます．

3.2.5.0.1 `trans_diff.r`

    1 "trans.diff" <-
    2 function(p, ei1, ei2=0, Ebb, Eg0,
    3         RL1, RL2=RL1, aRL1=RL1, aRL2=RL2, Ik, Rk)
    4 {
    5     # 差動増幅回路の伝達関数
    6     # p: パラメータ
    7     # eg: 入力電圧
    8     # Ebb: 電源電圧
    9     # Eg0: グリッド電圧
   10     # RL1: V1負荷抵抗(DC)
   11     # RL2: V2負荷抵抗(DC)
   12     # aRL1: V1負荷抵抗(AC)
   13     # aRL2: V2負荷抵抗(AC)
   14     # Ik: 共通カソード電流
   15     # Rk: カソード抵抗
   16 
   17     # check parameter
   18     if (missing(Ik) && missing(Rk))
   19         stop("Ik or Rk must be specified.")
   20     if (missing(Ik))
   21         mode <- 1       # mullard
   22     else
   23         mode <- 0       # diff
   24     
   25     if (length(ei1) != length(ei2)) {
   26         ei1 <- ei1 + ei2 * 0
   27         ei2 <- ei2 + ei1 * 0
   28     }
   29 
   30     get.ep.dc <- function(eg, ek, RL) {
   31         ip <- Ip(p, Ebb-ek, eg-ek)
   32         if (ip <= 0 || RL <= 0)
   33             return(list(ep=Ebb, ip=ip))
   34         ep <- uniroot(function(ep) {
   35             ip2 <- (Ebb - ep) / RL
   36             ip1 <- Ip(p, ep-ek, eg-ek)
   37             ip1 - ip2
   38         }, c(ek, Ebb))$root
   39         list(ep=ep, ip=(Ebb-ep)/RL)
   40     }
   41 
   42     get.ep.ac <- function(eg, ek, RL) {
   43         Epmax <- Ep0 + Ip0 * RL
   44         ip <- Ip(p, Epmax-ek, eg-ek)
   45         if (ip <= 0 || RL <= 0)
   46             return(list(ep=Ebb, ip=ip))
   47         ep <- uniroot(function(ep) {
   48             ip2 <- Ip0 + (Ep0 - ep) / RL
   49             ip1 <- Ip(p, ep-ek, eg-ek)
   50             ip1 - ip2
   51         }, c(ek, Epmax))$root
   52         list(ep=ep, ip=Ip0+(Ep0-ep)/RL)
   53     }
   54 
   55     f.dc <- function(ek) {
   56         if (mode == 1)
   57             ip <- ek / Rk
   58         else
   59             ip <- Ik
   60         v1 <- get.ep.dc(Eg0+eg1, ek, RL1)
   61         v2 <- get.ep.dc(Eg0+eg2, ek, RL2)
   62         v1$ip + v2$ip - ip
   63     }
   64 
   65     f.ac <- function(ek) {
   66         if (mode == 1)
   67             ip <- ek / Rk
   68         else
   69             ip <- Ik
   70         v1 <- get.ep.ac(Eg0+eg1, ek, aRL1)
   71         v2 <- get.ep.ac(Eg0+eg2, ek, aRL2)
   72         v1$ip + v2$ip - ip
   73     }
   74 
   75     if (mode == 1)
   76         ekmax <- Ebb * Rk / (Rk + RL1%p%RL2)
   77     else
   78         ekmax <- Ebb - Ik * min(c(RL1, RL2))
   79     cat("ekmax=", ekmax, "\n", sep="")
   80     eg1 <- eg2 <- 0
   81     ek0 <- uniroot(f.dc, c(Eg0, ekmax), tol=1e-8)$root
   82     cat("ek0=", ek0, "\n", sep="")
   83     v1 <- get.ep.dc(Eg0, ek0, RL1)
   84     Ep0 <- v1$ep
   85     Ip0 <- v1$ip
   86     cat("Ep0=", Ep0, ", Ip0=", Ip0, "\n", sep="")
   87 
   88     ek <- ip1 <- ip2 <- eo1 <- eo2 <- rep(NA, length(ei1))
   89     for (i in seq(along=ei1)) {
   90         cat(i, "")
   91         eg1 <- ei1[i]
   92         eg2 <- ei2[i]
   93         ek[i] <- uniroot(f.ac, c(min(c(eg1, eg2))+Eg0, ekmax), tol=1e-8)$root
   94         v1 <- get.ep.ac(Eg0+eg1, ek[i], aRL1)
   95         ip1[i] <- v1$ip
   96         eo1[i] <- v1$ep
   97         v2 <- get.ep.ac(Eg0+eg2, ek[i], aRL2)
   98         ip2[i] <- v2$ip
   99         eo2[i] <- v2$ep
  100     }
  101     cat("\n")
  102     list(ek=ek, eo1=eo1, eo2=eo2, ip1=ip1, ep1=eo1-ek, ip2=ip2, ep2=eo2-ek)
  103 }

trans.diff は，差動増幅回路およびカソード結合型位相反転回路の伝達特性を計算する関数です．差動増幅出力段にも使えるように，直流の負荷と交流の負荷として別々の値を指定することができます．

Ik または Rk のいずれか一方を指定します． Ik を指定した場合は差動増幅回路になり，値には共通カソード電流を指定します． Rk を指定した場合はカソード結合型位相反転回路になり，値には共通カソード抵抗を指定します．

> Ei <- seq(-20, 20, by=1)
> z <- trans.diff(t12AU7, ei1=Ei, Ebb=256, Eg=0, RL1=33e3, Ik=6.53632e-3)
> matplot(Ei, cbind(z$eo1, z$eo2), type="l", lty=1)

図3.18のようなグラフが描かれます．

**図 3.18:** 差動増幅回路の伝達特性
$\includegraphics{figs/diff4.ps}$

Next: 3.3 カソード結合型(ミュラード型) Up: 3. 位相反転回路 Previous: 3.1 P-K分割

Ayumi Nakabayashi
平成19年6月28日