Next: 4. 電力増幅回路(工事中) Up: 3. 位相反転回路 Previous: 3.2 差動増幅回路

3.3 カソード結合型(ミュラード型)

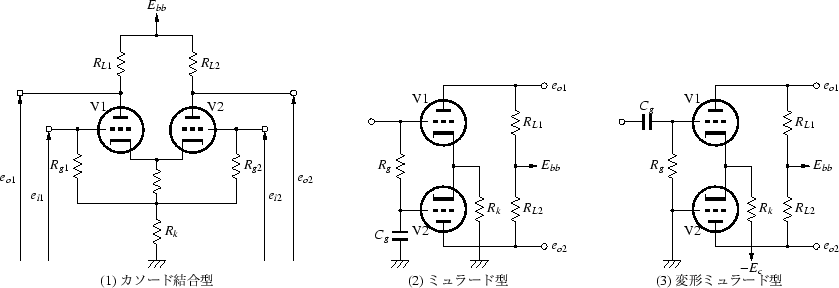
カソード結合型は，差動増幅回路の定電流源を高抵抗 R_k に変えたものです (図3.19 (1)参照)．差動増幅回路では，入力の約1/2がカソードに現われるため，定電流源ではなく R_k を使用すると共通カソード電流がわずかながら変動し， 2つの出力は対称ではなくなります．

ミュラード型は，カソードの電位が高くなることを利用して， V1のグリッドと前段のプレートを直結にしたものです(図3.19 (2))． V2のグリッドを直流的にはV1のグリッドの電位とし，交流的にはアースとするために， V2のグリッドは高抵抗 R_g を介してV1のグリッドに結び，また大容量の C_g でアースします．良好な低域特性を得るためには，この時定数を他の段間の時定数よりもかなり大きくしておきます．ミュラード型のほうが回路が簡潔になるので， (1)のカソード結合型が使われることはまずありません．

ミュラード型では，カソード電圧 E_k は増幅にほとんど寄与しておらず，大きな出力を得るためには，高い電源電圧 E_bb が必要になります．電源電圧が低い場合，図3.19 (3)のように，直結をあきらめて，グリッドの電位を0とし，カソード側を負の電源により引き込む回路を使うことがあります．この回路は，黒川達夫氏の作例[3,4]によく見られます．

**図 3.19:** カソード結合型・ミュラード型回路
$\begin{figure}\input{figs/mullard} \end{figure}$

3.3.1 ゲイン

ミュラード型位相反転回路の等価回路は図3.20のようになります．等価回路より，次の関係が成り立ちます．

**図 3.20:** ミュラード型回路の等価回路
$\begin{figure}\input{figs/mullard_equiv} \end{figure}$

μ₁e_g1	=	i₁(r_p1 + R_L1) + (i₁ + i₂)R_k	(3.31)
μ₂e_g2	=	i₂(r_p2 + R_L2) + (i₁ + i₂)R_k	(3.32)
e_i1	=	e_g1 + (i₁ + i₂)R_k	(3.33)
e_i2	=	e_g2 + (i₁ + i₂)R_k	(3.34)
e_o1	=	- i₁R_L1	(3.35)
e_o2	=	- i₂R_L2	(3.36)

これより， R₁ = r_p1 + R_L1, R₂ = r_p2 + R_L2 とおけば，

μ₁{e_i1 - (i₁ + i₂)R_k}	=	i₁R₁ + (i₁ + i₂)R_k
μ₂{e_i2 - (i₁ + i₂)R_k}	=	i₂R₂ + (i₁ + i₂)R_k
μ₁e_i1	=	i₁R₁ + (1 + μ₁)(i₁ + i₂)R_k
μ₂e_i2	=	i₂R₂ + (1 + μ₂)(i₁ + i₂)R_k
μ₁e_i1	=	{R₁ + (1 + μ₁)R_k}i₁ + (1 + μ₁)R_ki₂
μ₂e_i2	=	(1 + μ₂)R_ki₁ + {R₂ + (1 + μ₂)R_k}i₂
{R₂+(1+μ₂)R_k}μ₁e_i1-(1+μ₁)R_kμ₂e_i2
	=	{R₂ + (1 + μ₂)R_k}{R₁ + (1 + μ₁)R_k}i₁ - (1 + μ₁)(1 + μ₂)R_k²i₁
i₁	=	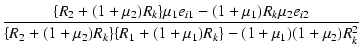$\displaystyle {\frac{{\{R_2+(1+\micro_2)R_k\}\micro_1 e_{i1} - (1+\micro_1)R_k ... ...R_2+(1+\micro_2)R_k\}\{R_1+(1+\micro_1)R_k\} - (1+\micro_1)(1+\micro_2)R_k^2}}}$
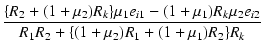	=	$\displaystyle {\frac{{\{R_2+(1+\micro_2)R_k\}\micro_1 e_{i1} - (1+\micro_1)R_k \micro_2 e_{i2}}}{{R_1 R_2 + \{(1+\micro_2)R_1+(1+\micro_1)R_2\}R_k}}}$
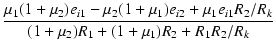	=	$\displaystyle {\frac{{\micro_1(1+\micro_2)e_{i1}-\micro_2(1+\micro_1)e_{i2}+\micro_1 e_{i1}R_2/R_k}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$
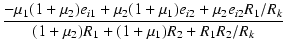i₂	=	$\displaystyle {\frac{{-\micro_1(1+\micro_2)e_{i1}+\micro_2(1+\micro_1)e_{i2}+\micro_2 e_{i2}R_1/R_k}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$
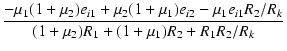e_o1	=	$\displaystyle {\frac{{-\micro_1(1+\micro_2)e_{i1}+\micro_2(1+\micro_1)e_{i2}-\micro_1 e_{i1}R_2/R_k}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$ R_L1	(3.37)
e_o2	=	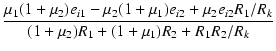$\displaystyle {\frac{{\micro_1(1+\micro_2)e_{i1}-\micro_2(1+\micro_1)e_{i2}+\micro_2 e_{i2}R_1/R_k}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$ R_L2	(3.38)

位相反転として用いるときは， e_i2 = 0 なので，

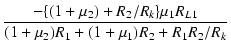A₁	=	$\displaystyle {\frac{{-\{(1+\micro_2) + R_2/R_k\} \micro_1 R_{L1}}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$	(3.39)
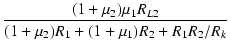A₂	=	$\displaystyle {\frac{{(1+\micro_2)\micro_1 R_{L2}}}{{(1+\micro_2)R_1+(1+\micro_1)R_2+R_1R_2/R_k}}}$	(3.40)

となります．特に， μ₁ = μ₂ = μ, r_p1 = r_p2 = r_p, R_L1 = R_L2 = R_L, R₁ = R₂ = R のとき，

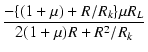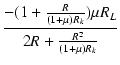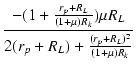A₁	=	$\displaystyle {\frac{{-\{(1+\micro) + R/R_k\} \micro R_L}}{{2(1+\micro)R+R^2/R_k}}}$ = $\displaystyle {\frac{{-(1+\frac{R}{(1+\micro)R_k})\micro R_L}}{{2R+\frac{R^2}{(1+\micro)R_k}}}}$ = $\displaystyle {\frac{{-(1+\frac{r_p+R_L}{(1+\micro)R_k})\micro R_L}}{{2(r_p+R_L)+\frac{(r_p+R_L)^2}{(1+\micro)R_k}}}}$	(3.41)
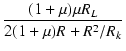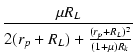A₂	=	$\displaystyle {\frac{{(1+\micro)\micro R_L}}{{2(1+\micro)R+R^2/R_k}}}$ = $\displaystyle {\frac{{\micro R_L}}{{2(r_p+R_L)+\frac{(r_p+R_L)^2}{(1+\micro)R_k}}}}$	(3.42)

ここで，正相側(V2)のゲインに対する逆相側(V1)のゲインの比を求めると，

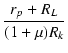
$\displaystyle {\frac{{\vert A_1\vert}}{{A_2}}}$ = 1 + $\displaystyle {\frac{{r_p+R_L}}{{(1+\micro)R_k}}}$

(3.43)

となります．すなわち，逆相側(V1)は正相側(V2)に比べて， m = (r_p + R_L)/((1 + μ)R_k) だけゲインが大きいということになります．これより，μ が高いほど，また R_k が高いほど，また R_L が低いほど，ACバランスが良くなることが分かります．

ACバランスに関して，「V2の負荷抵抗 R_L2をV1の負荷抵抗 R_L1 の 1 + m 倍して両側のゲインを揃えればよい」，という記述が多く見受けられますが，このようにしてもバランスは取れません． R_L2 を変えると，V1のゲインも変わってしまうからです．正しいACバランスを得るためには， | A₁| = A₂ を満たす R_L2 と R_L1 の関係を求めます．

\| A₁\|	=	A₂
{(1 + μ₂)R_k + (r_p2 + R_L2)}μ₁R_L1	=	(1 + μ₂)R_kμ₁R_L2
R_L2	=	$\displaystyle {\frac{{\{(1+\micro_2)R_k+r_{p2}\}R_{L1}}}{{(1+\micro_2)R_k - R_{L1}}}}$	(3.44)

このように R_L2 を定めれば，小信号時にACバランスが取れることになります．しかし，R_L2 を高くすると，V2のプレート電圧が下がり， V1の動作点とV2の動作点が異なってきます．それに伴って，三定数も多少ですが変わってきて，正負の対称性がくずれます．また，大振幅時には，V1, V2の非直線性も関わってくるため，正しいACバランスが維持されるとは限りません．

3.3.2 出力インピーダンス

**図 3.21:** ミュラード型回路の出力インピーダンスを求めるための等価回路
$\begin{figure}\input{figs/mullard_zo} \end{figure}$

e_o	=	i₁R_L1	(3.45)
e_k	=	(i₂ + i₃)R_k	(3.46)
e_g1	=	e_g2 = - e_k	(3.47)
e_o + μ₁e_g1	=	i₂r_p1 + (i₂ + i₃)R_k	(3.48)
μ₂e_g2	=	i₃(r_p2 + R_L2) + (i₂ + i₃)R_k	(3.49)

これより，

e_o - μ₁(i₂ + i₃)R_k	=	i₂r_p1 + (i₂ + i₃)R_k
e_o	=	{(1 + μ₁)R_k + r_p1}i₂ + (1 + μ₁)R_ki₃
- μ₂(i₂ + i₃)R_k	=	i₃(r_p2 + R_L2) + (i₂ + i₃)R_k
0	=	(1 + μ₂)R_ki₂ + {(1 + μ₂)R_k + r_p2 + R_L2}i₃
{(1 + μ₂)R_k + r_p2 + R_L2}e_o	=	[(1 + μ₂)R_kr_p1 + {(1 + μ₁)R_k + r_p1}(r_p2 + R_L2)]i₂
i₂	=	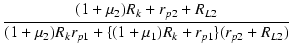$\displaystyle {\frac{{(1+\micro_2)R_k+r_{p2}+R_{L2}}}{{(1+\micro_2)R_k r_{p1}+\{(1+\micro_1)R_k+r_{p1}\}(r_{p2}+R_{L2})}}}$ e_o
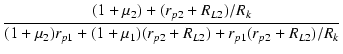	=	$\displaystyle {\frac{{(1+\micro_2)+(r_{p2}+R_{L2})/R_k}}{{(1+\micro_2)r_{p1}+(1+\micro_1)(r_{p2}+R_{L2})+r_{p1}(r_{p2}+R_{L2})/R_k}}}$
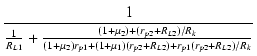Z_o	=	$\displaystyle {\frac{{e_o}}{{i_1+i_2}}}$ = $\displaystyle {\frac{{1}}{{\frac{1}{R_{L1}}+ \frac{(1+\micro_2)+(r_{p2}+R_{L2})... ... {(1+\micro_2)r_{p1}+(1+\micro_1)(r_{p2}+R_{L2})+r_{p1}(r_{p2}+R_{L2})/R_k} }}}$
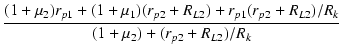	=	R_L1// $\displaystyle {\frac{{(1+\micro_2)r_{p1}+(1+\micro_1)(r_{p2}+R_{L2})+r_{p1}(r_{p2}+R_{L2})/R_k}}{{(1+\micro_2)+(r_{p2}+R_{L2})/R_k}}}$	(3.50)

3.3.3 数値例

ここでは，12AU7を使ったミュラード型位相反転回路を解析します．電源電圧 E_bb = 350 V, 負荷抵抗 R_L = 33 kΩ, カソード抵抗 15.3 kΩ, 対アースグリッド電圧 E_ge = 94 V とします．動作点は， E_p = 142.1451 V, E_g = - 6.00566 V, I_p = 3.26816 mA で，この動作点における三定数は， g_m = 1388.774 μS, r_p = 11.75587 kΩ, μ = 16.32624 です．

R₁	=	R₂ = 44.75587 [kΩ]
A₁	=	- 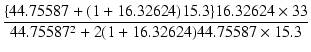$\displaystyle {\frac{{\{44.75587+(1+16.32624)15.3\}16.32624\times 33}}{{44.75587^2+2(1+16.32624)44.75587\times 15.3}}}$ = - 6.487483
A₂	=	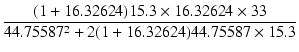$\displaystyle {\frac{{(1+16.32624)15.3\times 16.32624\times 33}}{{44.75587^2+2(1+16.32624)44.75587\times 15.3}}}$ = 5.5504
Z_o	=	33//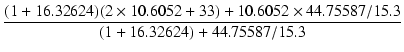 $\displaystyle {\frac{{(1+16.32624)(2\times 10.6052+33)+10.6052\times44.75587/15.3}}{{(1+16.32624)+44.75587/15.3}}}$ = 19.88694 [kΩ]

この定数で差動増幅回路を構成した場合の出力インピーダンスは 20.834 kΩ ですから，ミュラード型にすると出力インピーダンスが多少下がります．しかし計算が面倒なので，近似値として差動増幅回路の出力インピーダンスを求めるほうがよいでしょう．

図3.22に， V1およびV2のプレートに 100 pF または 0.01 μF を付加した場合の周波数特性を示します．赤い線がV1側のゲイン，青い線がV2側のゲインを表わしています．実線は，V1，V2とも 100 pF を付加した場合，破線は，V1に 100 pF, V2に 0.01 μF を付加した場合，点線は，V1に 0.01 μF, V2に 100 pF を付加した場合，一点鎖線は，V1，V2とも 0.01 μF を付加した場合です．

**図 3.22:** ミュラード型位相反転回路の周波数特性(1)
$\includegraphics{figs/mullard1.ps}$

V1側に 220 pF, V2側に 200 pF を付加した場合の周波数特性は図3.7のようになります．ごくわずかですが周波数特性にコブができていて，差動増幅回路よりもクセがあることがわかります．

**図 3.23:** ミュラード型位相反転回路の周波数特性(2)
$\includegraphics{figs/mullard2.ps}$

3.3.4 シミュレーション例

さきほどの数値例の定数を使い，SPICEでシミュレートします．回路は，図3.24のとおりです．

**図 3.24:** ミュラード型位相反転回路(シミュレーション用)
$\begin{figure}\input{figs/mullard_spice} \end{figure}$

3.3.4.1 `mullard.cir`

    1 Mullard type phase inverter with 12AU7
    2 .INCLUDE 12AU7.lib
    3 .OPTIONS ITL1=200 ITL2=200
    4 X1 1 2 3 12AU7
    5 X2 4 5 3 12AU7
    6 RK 3 0 15.3k
    7 RL1 6 1 33k
    8 RL2 6 4 33k
    9 RG1 2 0 470k
   10 RG2 5 0 470k
   11 VI1 2 0 DC 94V
   12 VI2 5 0 DC 94V
   13 VBB 6 0 350V
   14 .control
   15 op
   16 print v(1) v(3) v(1,3) v(2,3) v(4,3) v(5,3) i(vbb)
   17 tf v(1) vi1
   18 print all
   19 tf v(4) vi1
   20 print all
   21 .endc
   22 .END

3.3.4.2 結果

    1 
    2 Circuit: Mullard type phase inverter with 12AU7
    3 
    4 v(1) = 2.421508e+02
    5 v(3) = 1.000057e+02
    6 v(1,3) = 1.421451e+02
    7 v(2,3) = -6.00566e+00
    8 v(4,3) = 1.421451e+02
    9 v(5,3) = -6.00566e+00
   10 i(vbb) = -6.53632e-03
   11 transfer_function = -6.48748e+00
   12 output_impedance_at_v(1) = 1.988694e+04
   13 vi1#input_impedance = 4.700000e+05
   14 transfer_function = 5.550397e+00
   15 output_impedance_at_v(4) = 1.988694e+04
   16 vi1#input_impedance = 4.700000e+05

3.3.5 設計

ミュラード型位相反転回路のロードラインは，図3.17のようになります．青い線が負荷抵抗 33 kΩ によるロードラインで， x 軸との交点は E_bb = 350 V にとってあるので，各球の対アースプレート電圧を表わします． V1のロードラインは緑色の線(丸印がついている曲線)で， V2のロードラインは茶色の線です． V1のプレート電流とカソード電圧の関係は，オレンジ色の線で表わされています．

**図 3.25:** ミュラード型位相反転回路のロードライン
$\includegraphics{figs/mullard5.ps}$

例えば e_i = 10 V の入力があった場合，カソード電圧は E_k = 104.9 V となり， V1のグリッド電圧は E_g1 = 94 + 10 - 104.9 = - 0.9 V となって，プレート電流が I_p1 = 5.29 mA 流れます．このときのプレート電圧は E_p1 = 70.6 V で，対アースプレート電圧は E_o1 = 175.5 V になります． V2のグリッド電圧は E_g2 = 94 - 104.9 = - 10.9 V となって，プレート電流が I_p2 = 1.57 mA 流れます．このときのプレート電圧は E_p2 = 175.5 V で，対アースプレート電圧は E_o2 = 298.3 V になります．プレート電流の合計は 5.29 + 1.57 = 6.86 mA となって，無信号時のカソード電流 6.54 mA より増えています．

また，V1のロードラインと E_g = 0 の交点は，約 12 V なので，尖頭値で 12 V までの入力を加えることができます．

伝達特性のグラフは，差動増幅回路と同様にRの関数 trans.diff を使用して作成できます．

> Ei <- seq(-20, 20, by=1)
> z <- trans.diff(t12AU7, ei1=Ei, Ebb=350, Eg=94, RL1=33e3, Rk=15.3e3)
> matplot(Ei, cbind(z$eo1, z$eo2), type="l", lty=1)

図3.26のようなグラフが描かれます．点線は，V1の出力を反転したもので，V1のゲインが大きいことがわかります．

**図 3.26:** ミュラード型位相反転回路の伝達特性
$\includegraphics{figs/mullard6.ps}$

3.3.6 ACバランスの調整例

式(3.44)の R_L1, R_L2 には，交流負荷抵抗，すなわちプレート抵抗と次段のグリッド抵抗との並列抵抗値を用います．プレート抵抗，カソード抵抗等は数値例の定数とし，次段のグリッド抵抗を 100 kΩ とした場合の R_p2 を求めてみましょう．

R_L1 = R_p1//R_g1 = 33//100 = 24.81203 [kΩ]

より，

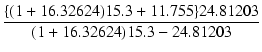R_L2	=	$\displaystyle {\frac{{\{(1+16.32624)15.3+11.755\}24.81203}}{{(1+16.32624)15.3-24.81203}}}$ = 28.58815 [kΩ]	(3.51)
R_p2	=	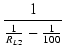$\displaystyle {\frac{{1}}{{\frac{1}{R_{L2}}-\frac{1}{100}}}}$ = 40.03278 [kΩ]	(3.52)

となります．この定数でシミュレートした結果を図3.27に示します．また，この定数の場合のロードラインを図3.28に，伝達特性を図3.29に示します．

**図 3.27:** ミュラード型のACバランス
$\includegraphics{figs/mullard3.ps}$

**図 3.28:** ACバランスをとった場合のロードライン
$\includegraphics{figs/mullard7.ps}$

**図 3.29:** ACバランスをとった場合の伝達特性
$\includegraphics{figs/mullard8.ps}$

3.3.6.1 `mullard3.cir`

    1 Mullard type phase inverter with 12AU7
    2 .INCLUDE 12AU7.lib
    3 X1 1 2 3 12AU7
    4 X2 4 5 3 12AU7
    5 RK 3 0 15.3k
    6 RL1 6 1 33k
    7 RL2 6 4 40.03278k
    8 RG1 2 0 470k
    9 RG2 5 0 470k
   10 VI1 2 0 DC 94V AC 1V
   11 VI2 5 0 DC 94V
   12 VBB 6 0 350V
   13 CC1 1 7 1u
   14 CC2 4 8 1u
   15 RG3 7 0 100k
   16 RG4 8 0 100k
   17 CS1 7 0 100p
   18 CS2 8 0 100p
   19 .control
   20 ac dec 20 1 1Meg
   21 print db(v(7)) db(v(8))
   22 .endc
   23 .END

プレート抵抗が増えたことによって，動作点が変化して，バイアスが浅くなっています．

伝達特性のグラフでは，プレートの電圧ではなく，信号成分のみをとりだして(動作点のプレート電圧を引いて)描いています．尖頭値で 50 V 程度までは両相の出力がよく揃っていますが，それ以上の出力を取り出すとバランスがくずれていきます．

従来の方法で R_p2 を計算すると，

m	=	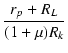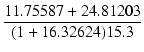$\displaystyle {\frac{{r_p+R_L}}{{(1+\micro)R_k}}}$ = $\displaystyle {\frac{{11.75587+24.81203}}{{(1+16.32624)15.3}}}$ = 0.1379445
R_L2	=	R_L1(1 + m) = 24.81203(1 + 16.32624) = 28.23471 [kΩ]
R_p2	=	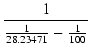$\displaystyle {\frac{{1}}{{\frac{1}{28.23471}-\frac{1}{100}}}}$ = 39.34313 [kΩ]

となります．この定数でシミュレートした結果を図3.30に示します．

**図 3.30:** ミュラード型のACバランス(従来型)
$\includegraphics{figs/mullard4.ps}$

3.3.6.2 `mullard4.cir`

    1 Mullard type phase inverter with 12AU7
    2 .INCLUDE 12AU7.lib
    3 X1 1 2 3 12AU7
    4 X2 4 5 3 12AU7
    5 RK 3 0 15.3k
    6 RL1 6 1 33k
    7 RL2 6 4 39.34313k
    8 RG1 2 0 470k
    9 RG2 5 0 470k
   10 VI1 2 0 DC 94V AC 1V
   11 VI2 5 0 DC 94V
   12 VBB 6 0 350V
   13 CC1 1 7 1u
   14 CC2 4 8 1u
   15 RG3 7 0 100k
   16 RG4 8 0 100k
   17 CS1 7 0 100p
   18 CS2 8 0 100p
   19 .control
   20 ac dec 20 1 1Meg
   21 print db(v(7)) db(v(8))
   22 .endc
   23 .END

Next: 4. 電力増幅回路(工事中) Up: 3. 位相反転回路 Previous: 3.2 差動増幅回路

Ayumi Nakabayashi
平成19年6月28日