next up previous index
Next: B.2 五極管のモデル Up: B. 真空管のモデル Previous: B. 真空管のモデル

B.1 三極管のモデル

B.1.1 特性曲線の特徴

「オーディオ用真空管マニュアル」[1]によれば， 三極管の特性曲線には次のような特徴があります．
  1. バイアスが0Vのときよりも， -0.5 $ \sim$ - 0.8Vくらい負のときのほうが， 原点を通る曲線に近くなっている．
  2. カットオフのところの $ \mu$ ($ \mu_{c}^{}$)は プレート電圧のいかんによらず一定である．
  3. バイアスのうんと浅いところでは $ \mu$ は一定であって， このときの $ \mu$ を $ \mu_{m}^{}$ とすれば $ \mu_{m}^{}$ = 1.5$ \mu_{c}^{}$ に近い．
  4. プレート電圧が一定のときの gm は， ほぼプレート電流 Ip の0.6乗に比例する．
  5. Ep/Eg が一定なら $ \mu$ が一定である．
これらの性質を満たす関数 Ip(Ep, Eg) は次のようになります．

Ip(Ep, Eg) = G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigl)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigl)$Ep$\displaystyle \Bigl\}^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigl)^{{\frac{1}{1-\alpha}}}_{}$ (B.1)
ここで， Egg = Eg + 0.6 で， $ \alpha$ は約0.6です． 上の式は， Egg$ \le$ 0 かつ Ep$ \ge$ - $ \mu_{c}^{}$Egg の範囲で 近似的に成り立ちます．

B.1.2 三定数

この式から三定数を求めます． 相互コンダクタンス gm は，
gm = $\displaystyle {\frac{{\partial I_p}}{{\partial E_g}}}$  
  = $\displaystyle {\frac{{1}}{{1-\alpha}}}$G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)$Ep$\displaystyle \Bigr\}^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}-1}}_{}$ (B.2)
  = $\displaystyle {\frac{{I_p}}{{1-\alpha}}}$ . $\displaystyle {\frac{{1}}{{E_{gg} + \frac{E_p}{\mu_c}}}}$ (B.3)

内部抵抗 rp を直接求めるのは難しいので， rp の逆数を求めます．
$\displaystyle {\frac{{1}}{{r_p}}}$ = $\displaystyle {\frac{{\partial I_p}}{{\partial E_p}}}$  
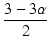  = G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle {\frac{{3}}{{2}}}$ - $\displaystyle {\frac{{1}}{{1-\alpha}}}$$\displaystyle \Bigr)$Ep$\scriptstyle {\frac{{3}}{{2}}}$-$\scriptstyle {\frac{{1}}{{1-\alpha}}}$-1$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$  
      + Ep$\scriptstyle {\frac{{3}}{{2}}}$-$\scriptstyle {\frac{{1}}{{1-\alpha}}}$$\displaystyle {\frac{{1}}{{1-\alpha}}}$ . $\displaystyle {\frac{{1}}{{\mu_c}}}$$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}-1}}_{}$$\displaystyle \Bigr\}$  
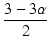  = G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$Ep$\scriptstyle {\frac{{3}}{{2}}}$-$\scriptstyle {\frac{{1}}{{1-\alpha}}}$$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$  
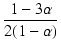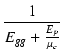      x $\displaystyle \Bigl\{$$\displaystyle {\frac{{1-3\alpha}}{{2(1-\alpha)}}}$ . $\displaystyle {\frac{{1}}{{E_p}}}$ + $\displaystyle {\frac{{1}}{{1-\alpha}}}$ . $\displaystyle {\frac{{1}}{{\mu_c}}}$ . $\displaystyle {\frac{{1}}{{E_{gg} + \frac{E_p}{\mu_c}}}}$$\displaystyle \Bigr\}$  
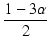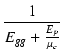  = $\displaystyle {\frac{{I_p}}{{1-\alpha}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{1-3\alpha}}{{2}}}$ . $\displaystyle {\frac{{1}}{{E_p}}}$ + $\displaystyle {\frac{{1}}{{\mu_c}}}$ . $\displaystyle {\frac{{1}}{{E_{gg} + \frac{E_p}{\mu_c}}}}$$\displaystyle \Bigr)$ (B.4)

最後に増幅率 $ \mu$ は，gm と rp の積で求めます．
$\displaystyle \mu$ = gmrp = $\displaystyle {\frac{{1}}{{E_{gg} + \frac{E_p}{\mu_c}}}}$ . $\displaystyle {\frac{{1}}{{\frac{1-3\alpha}{2} \cdot \frac{1}{E_p} + \frac{1}{\mu_c} \cdot \frac{1}{E_{gg}+\frac{E_p}{\mu_c}}}}}$  
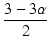
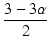
  = $\displaystyle {\frac{{1}}{{\big(\frac{E_{gg}}{E_p}+\frac{1}{\mu_c}\big)\frac{1-3\alpha}{2} + \frac{1}{\mu_c}}}}$ = $\displaystyle {\frac{{1}}{{\displaystyle \frac{3-3\alpha}{2} \cdot \frac{1}{\mu_c} + \frac{1-3\alpha}{2} \cdot \frac{E_{gg}}{E_p}}}}$ (B.5)

ここで，前述した三極管の特性曲線の特徴が満たされているか，調べてみます． まず，1ですが， 式(B.1)より， プレート電流 Ip は Eg = - 0.6 のときに Ep の1.5乗に比例します．

2に関してですが， カットオフのところでは， 式(B.1)より Egg + Ep/$ \mu_{c}^{}$ = 0 ですから， $ \mu$ は $ \mu_{c}^{}$ となります．

3については， 式(B.5)の Egg に0を代入すると，これが $ \mu_{m}^{}$ となり，

$\displaystyle \mu_{m}^{}$ = $\displaystyle {\frac{{2}}{{3 - 3\alpha}}}$$\displaystyle \mu_{c}^{}$ $\displaystyle \approx$ 1.67$\displaystyle \mu_{c}^{}$ (B.6)
となります．

4の関係が成立するかどうかを調べます． 式(B.1), (B.2)を Egg + Ep/$ \mu_{c}^{}$ について解きます． 式(B.1)より，

Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$ = $\displaystyle {\frac{{I_p^{1-\alpha}}}{{\displaystyle G^{1-\alpha}\frac{3-3\al... ...mu_c}-\frac{1}{\mu_m}\Bigr)^{\frac{1-3\alpha}{2}} E_p^{\frac{1-3\alpha}{2}}}}}$ (B.7)
式(B.2)より，

Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$ = $\displaystyle {\frac{{\{(1-\alpha) g_m\}^{\frac{1-\alpha}{\alpha}}}}{{\displays... ...1}{\mu_m}\Bigr)^{\frac{1-3\alpha}{2\alpha}} E_p^{\frac{1-3\alpha}{2\alpha}}}}}$ (B.8)
式(B.7)と式(B.8)の右辺が等しいとおき， gm について解くと，
{(1 - $\displaystyle \alpha$)gm}$\scriptstyle {\frac{{1-\alpha}}{{\alpha}}}$ = $\displaystyle {\frac{{\displaystyle G^{\frac{1-\alpha}{\alpha}} \Bigl(\frac{3-3... ...\mu_c}-\frac{1}{\mu_m}\Bigr)^{\frac{1-3\alpha}{2}} E_p^{\frac{1-3\alpha}{2}}}}}$Ip1-$\scriptstyle \alpha$  
  = G$\scriptstyle {\frac{{(1-\alpha)^2}}{{\alpha}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1-\alpha}{\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{(1-3\alpha)(1-\alpha)}{2\alpha}}}_{}$Ep$\scriptstyle {\frac{{(1-3\alpha)(1-\alpha)}}{{2\alpha}}}$Ip1-$\scriptstyle \alpha$  
gm = $\displaystyle {\frac{{3}}{{2}}}$Ip$\scriptstyle \alpha$G1-$\scriptstyle \alpha$Ep$\scriptstyle {\frac{{1}}{{2}}}$-$\scriptstyle {\frac{{3}}{{2}}}$$\scriptstyle \alpha$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{1}{2}-\frac{3}{2}\alpha}}_{}$ (B.9)

式(B.9)は，[1, p. 124]に記載されている式ですB.1．

5は，式(B.5)より明らかです．

B.1.3 三極管のグリッド電流モデル

B.1.3.1 グリッドが正の場合のカソード電流

これまでは Egg$ \le$ 0 の場合について考えてきましたが， ここで，Egg > 0 の場合を考えます． Egg > 0 の場合，インゼル効果B.2を考えなくてもよいので，$ \mu$ は $ \mu_{m}^{}$ で一定と仮定します．

三極管のカソードから流れる電流は， グリッドの位置にプレートがある二極管(等価二極管)を考え， そのプレート電圧(有効電圧)を

Est = Egg + $\displaystyle {\frac{{E_p}}{{\mu_m}}}$ (B.10)
として考えます． グリッド電圧が正の領域ではインゼル効果を考える必要がないので， 等価二極管のプレート電流(カソード電流)は，プレート電圧の1.5乗に比例します． したがって，カソード電流は，

Ik = G'Est1.5 = G'$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_m}}}$$\displaystyle \Bigr)^{{1.5}}_{}$ (B.11)
と表せます． ここで，G' は等価二極管のパービアンスです．

G' を求めます． Egg = 0 のときの Ip は，式(B.1)より，

Ip = G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$Ep3/2

で， Egg = 0 のときの Ik は，式(B.11)より

Ik = G'$\displaystyle \Bigl($$\displaystyle {\frac{{E_p}}{{\mu_m}}}$$\displaystyle \Bigr)^{{1.5}}_{}$

で，両者が一致するので，

G' = G$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$$\displaystyle \Bigr)^{{\frac{1}{1-\alpha}}}_{}$$\displaystyle \mu_{m}^{{3/2}}$

式(B.6)を用いて，
G' = G$\displaystyle \mu_{m}^{{-\frac{1}{1-\alpha}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$$\displaystyle \mu_{m}^{{3/2}}$  
  = G$\displaystyle \Bigl\{$$\displaystyle \mu_{m}^{}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigr)$$\displaystyle \Bigr\}^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$ = G$\displaystyle \Bigl($$\displaystyle {\frac{{\mu_m}}{{\mu_c}}}$ -1$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$  
  = G$\displaystyle \Bigl($$\displaystyle {\frac{{3\alpha-1}}{{3-3\alpha}}}$$\displaystyle \Bigr)^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$ (B.12)

となります．

グリッド電圧を変えた場合の，プレート電圧とカソード電流の関係をグラフに表すと， 図B.1のようになります．

図 B.1: 等価二極管のカソード電流
\begin{figure}\input{figs/ig_1} \end{figure}
グリッド電圧が 0V のときは，プレート電圧が 0V のところから プレート電流が流れ始めます． グリッド電圧が Eg (> 0)のときは， プレート電圧が - $ \mu$Eg のところからプレート電流が流れ始めます． もちろん，実際にはプレート電圧が正でなければプレート電流は流れないので， グラフの第二象限には意味がありません． プレート電圧がグリッド電圧より十分に大きな領域では， カソード電流としてこの式を使います．

B.1.3.2 プレート電流の最大値

次に，プレート電圧とカソード電圧が等しい場合， すなわち二極管接続の場合を考えます． この場合，グリッド電流とプレート電流の比は，プレート電圧(グリッド電圧)にかかわらずほぼ一定です． カソード電流に対するグリッド電流の比を xg とします．

xg $\displaystyle \equiv$ $\displaystyle {\frac{{I_g}}{{I_k}}}$$\displaystyle \Bigr\vert _{{E_p=E_g}}^{}$ (B.13)
図B.2に801のプレート特性図を示しますが， Ep < Eg の場合は，Ep = Eg のカーブを超えたプレート電流が流れることはありません．

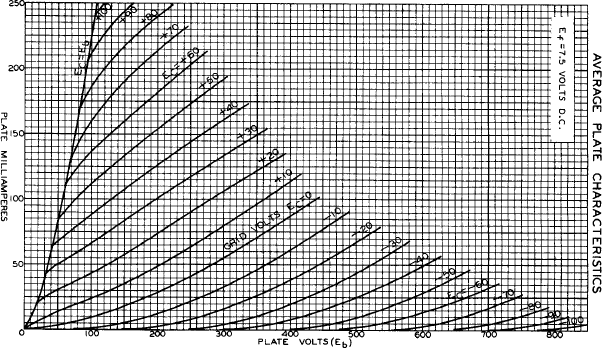
801_plate.png

図 B.2: 801のプレート特性図
\begin{figure}. % \end{figure}
また Ep = Eg のカーブはプレート電圧の1.5乗に比例しています． これらから，プレート電圧を与えた時に流れうる最大のプレート電流 Ip lim を次の式で表すことができます．

Ip lim = (1 - xg)GlimEp1.5 (B.14)
ここで，Glim はプレート電流を制限する一種のパービアンスと考えられます．

この xg および Glim は， Ep* = Eg* のプレート電流 Ip* および グリッド電流 Ig* のデータがあればそれを用いて，

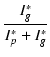xg = $\displaystyle {\frac{{I_g^*}}{{I_p^*+I_g^*}}}$ (B.15)
Glim = 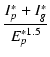$\displaystyle {\frac{{I_p^*+I_g^*}}{{E_p^{*1.5}}}}$ (B.16)

で求めます． グリッド電流のデータがない場合の求め方は後述します．

B.1.3.3 グリッド電流とプレート電圧の関係

Ep$ \ge$Eg のとき，カソードから放出された電子はグリッドおよびプレートによって 作られる電界によって加速され，一部はグリッドに流れ込み，残りはさらに加速されてプレートに流れます． プレート電圧が高くなればなるほど，グリッドに流れ込む電流は少なくなります．

Ep < Eg のとき，グリッドを通り過ぎた電子は，グリッド-プレート間の電界によって減速させられ，一部はプレートに到達しますが，グリッドに戻ってくる電子もあります． したがって，プレート電圧が低くなればなるほど，グリッド電流が増えます．

このようすを表すのが関数 fg(Ep) で， Ep = Eg のときのグリッド電流を基準として， さまざまなプレート電圧に対するグリッド電流の相対的な大きさを表しています(図B.3)．

fg(Ep) = 1.2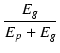$\displaystyle {\frac{{E_g}}{{E_p+E_g}}}$ + 0.4 (B.17)
図 B.3: プレート電圧に対するグリッド電流の変化
\begin{figure}\input{figs/ig_3} \end{figure}
この関数は，Ep = 0 のとき，1.6 となり， Ep $ \gg$ Eg のとき，0.4 となります． この関数を用いて，グリッド電流は次のように表せます．

Ig = xgGlimEg1.5fg(Ep) (B.18)

ここで，グリッド電流のデータがない場合のグリッド電流の推定方法を述べます． プレート電圧がグリッド電圧より高い場合， カソード電流は図B.4の Ik のカーブのようになります(式(B.11))．

図 B.4: カソード電流とグリッド電流
\begin{figure}\input{figs/ig_4} \end{figure}
プレート電圧が0となった場合， カソード電流はグリッド電流と等しく，Ik のカーブとy軸の交点 Ik0 よりも低くなります． ここで，経験的に，

Ig0 = 0.8Ik0 (B.19)
とします． したがって，

Ig1 = $\displaystyle {\frac{{I_{g0}}}{{1.6}}}$ = 0.5Ik0

となります．

式(B.11)を使って Ik0, Ik1, Ig1 を求めると，

Ik0 = G'Eg1.5  
Ik1 = G'$\displaystyle \Bigl($Eg + $\displaystyle {\frac{{E_g}}{{\mu}}}$$\displaystyle \Bigr)^{{1.5}}_{}$ = G'$\displaystyle \Bigl($1 + $\displaystyle {\frac{{1}}{{\mu}}}$$\displaystyle \Bigr)^{{1.5}}_{}$Eg1.5  
Ig1 = 0.5Ik0 = 0.5G'Eg1.5  

これらより，
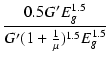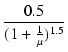xg = $\displaystyle {\frac{{I_{g1}}}{{I_{k1}}}}$ = $\displaystyle {\frac{{0.5 G' E_g^{1.5}}}{{G' (1 + \frac{1}{\mu})^{1.5} E_g^{1.5}}}}$ = $\displaystyle {\frac{{0.5}}{{(1 + \frac{1}{\mu})^{1.5}}}}$ (B.20)
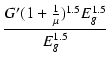Glim = $\displaystyle {\frac{{I_{k1}}}{{E_g^{1.5}}}}$ = $\displaystyle {\frac{{G' (1 + \frac{1}{\mu})^{1.5} E_g^{1.5}}}{{E_g^{1.5}}}}$ = G'$\displaystyle \Bigl($1 + $\displaystyle {\frac{{1}}{{\mu}}}$$\displaystyle \Bigr)^{{1.5}}_{}$ (B.21)

のように推定できます．

B.1.3.4 プレート電流

プレート電流は，カソード電流からグリッド電流を引いたもので， 式(B.14)を超えないよう制限されます(図B.5)．

Ip = min(Ik - Ig, Ip lim) (B.22)
図 B.5: プレート電流
\begin{figure}\input{figs/ig_5} \end{figure}

B.1.4 まとめ

これまで Egg は Eg よりも約 0.6V 高いとしていましたが， この値も真空管により異なるので，これを Ego とします．

Egg = Eg + Ego (B.23)
また，
a = $\displaystyle {\frac{{1}}{{1-\alpha}}}$ (B.24)
b = $\displaystyle {\frac{{3}}{{2}}}$ - a = $\displaystyle {\frac{{3}}{{2}}}$ - $\displaystyle {\frac{{1}}{{1-\alpha}}}$ (B.25)
c = 3$\displaystyle \alpha$ - 1 (B.26)

とおくと，
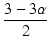$\displaystyle \Bigl($$\displaystyle {\frac{{3-3\alpha}}{{2}}}$$\displaystyle \Bigl)^{{\frac{1}{1-\alpha}}}_{}$ = $\displaystyle \Bigl($$\displaystyle {\frac{{3}}{{2a}}}$$\displaystyle \Bigr)^{a}_{}$  
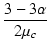$\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{1}}{{\mu_m}}}$$\displaystyle \Bigl)$Ep$\displaystyle \Bigl\}^{{\frac{3}{2}-\frac{1}{1-\alpha}}}_{}$ = $\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{\mu_c}}}$ - $\displaystyle {\frac{{3-3\alpha}}{{2\mu_c}}}$$\displaystyle \Bigr)$Ep$\displaystyle \Bigr\}^{b}_{}$ = $\displaystyle \Bigl\{$$\displaystyle \Bigl($1 - $\displaystyle {\frac{{3}}{{2a}}}$$\displaystyle \Bigr)$$\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr\}^{b}_{}$  
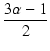  = $\displaystyle \Bigl($$\displaystyle {\frac{{3\alpha - 1}}{{2}}}$ . $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{b}_{}$ = $\displaystyle \Bigl($$\displaystyle {\frac{{c}}{{2}}}$ . $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{b}_{}$  

となるので， 式(B.1)は次のように書けます．

Ip = G$\displaystyle \Bigl($$\displaystyle {\frac{{3}}{{2a}}}$$\displaystyle \Bigl)^{a}_{}$$\displaystyle \Bigl($$\displaystyle {\frac{{c}}{{2}}}$ . $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigr)^{b}_{}$$\displaystyle \Bigl($Egg + $\displaystyle {\frac{{E_p}}{{\mu_c}}}$$\displaystyle \Bigl)^{a}_{}$

また，式(B.12)は次のように書けます．

G' = G$\displaystyle \Bigl($$\displaystyle {\frac{{ac}}{{3}}}$$\displaystyle \Bigr)^{b}_{}$ (B.27)

これらを使って，これまでの式をまとめます．

Ik = $\displaystyle \left\{\vphantom{ \begin{array}{ll} G \bigl(\frac{3}{2a}\bigl)^a ... ...rac{E_p}{\mu_m}\bigl)^{1.5}, & \mbox{$E_{gg} > 0$ のとき} \end{array} }\right.$$\displaystyle \begin{array}{ll} G \bigl(\frac{3}{2a}\bigl)^a \bigl(\frac{c}{2} ... ...{gg} + \frac{E_p}{\mu_m}\bigl)^{1.5}, & \mbox{$E_{gg} > 0$ のとき} \end{array}$ (B.28)
Ig = $\displaystyle \left\{\vphantom{ \begin{array}{ll} 0, & \mbox{$E_g \le 0$ のと�... ...frac{E_g}{E_p+E_g} + 0.4\bigr), & \mbox{$E_g < 0$ のとき} \end{array} }\right.$$\displaystyle \begin{array}{ll} 0, & \mbox{$E_g \le 0$ のとき} \\ x_g G_{\lim... ...igl(1.2 \frac{E_g}{E_p+E_g} + 0.4\bigr), & \mbox{$E_g < 0$ のとき} \end{array}$ (B.29)
Ip lim = (1 - xg)GlimEp1.5 (B.30)
Ip = min(Ik - Ig, Ip lim) (B.31)

next up previous index
Next: B.2 五極管のモデル Up: B. 真空管のモデル Previous: B. 真空管のモデル
Ayumi Nakabayashi
平成19年6月28日